Bạn đang xem : Công thức tính đường cao trong tam giác đều dễ nhớ nhất
Công thức tính đường cao trong tam giác đều dễ nhớ nhất được cập nhật mới nhất tại Tamthethanglong.com. Trang thông tin tổng hợp mới nhất của giới trẻ hiện nay, cập nhật liên tục.
Bạn chưa biết cách tính đường cao trong tam giác đều? Đừng quá lo lắng, bài viết sau của TamTheThangLong sẽ bật mí giúp bạn công thức tính đường cao trong tam giác đều. Mời bạn đọc tham khảo bài viết sau đây để biết rõ hơn.
Đường cao trong tam giác đều là gì?
Tam giác đều là gì?
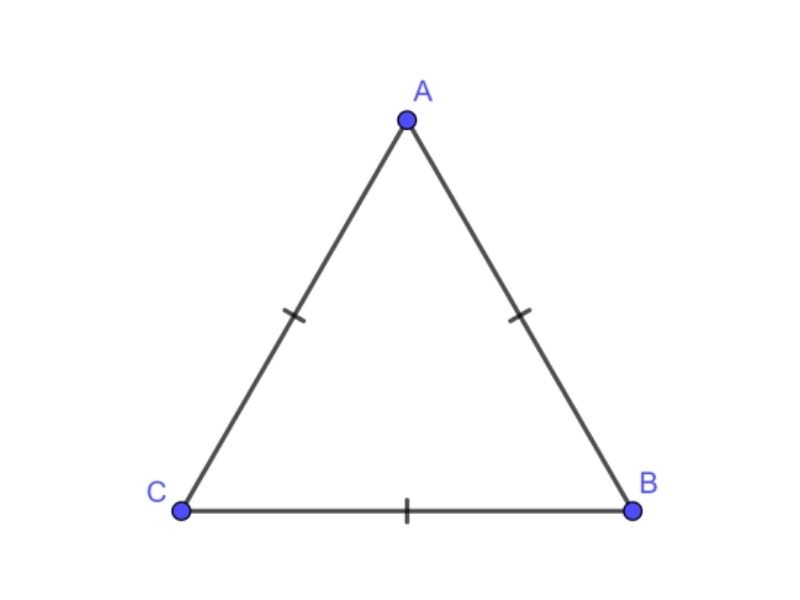
Trong hình học, tam giác đều được định nghĩa là tam giác có ba cạnh bằng nhau hoặc tương đương ba góc bằng nhau. Đồng thời mỗi góc bằng 60 độ. Tam giác đều hay còn gọi là đa giác đều với số cạnh bằng ba.
Sau khi biết khái niệm về tam giác đều, mời bạn đến nội dung tiếp theo của bài viết. Đó là đường cao trong tam giác đều là gì. Mời bạn đọc tham khảo nội dung sau để biết thêm chi tiết.
Xem thêm : Cách tính chu vi hình tam giác – Giải bài tập SGK Toán 3
Đường cao trong tam giác đều là gì?
Đường cao trong tam giác đều là đoạn thẳng kẻ từ đỉnh của tam giác vuông góc với cạnh đáy. Độ dài của đường cao cũng chính là độ dài của đường thẳng đó.
Đường cao trong tam giác đều là đường trung trực chia cạnh đối diện thành hai phần bằng nhau. Đồng thời, đường cao trong tam giác đều cũng chính là đường phân giác ở đỉnh tam giác và đường trung tuyến.
Bên cạnh đó, đường cao của tam giác đều chia góc ở đỉnh thành hai góc có số đo bằng nhau. Ngoài ra, đường cao trong tam giác đều sẽ chia tam giác đó thành hai tam giác vuông bằng nhau.
Tham khảo thêm : 520 là gì? Ý nghĩa ngọt ngào của con số 520 trong tình yêu
Đường cao của một tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được xem là đáy ứng với chiều cao. Độ dài của đường cao là khoảng cách từ đỉnh đến đáy. Mỗi tam giác gồm có 3 đường cao.
Vừa rồi là định nghĩa về đường cao trong tam giác đều. Tiếp nối bài viết là phần nội dung quan trọng, cách tính đường cao trong tam giác đều. Mời bạn đọc tham khảo nội dung sau cùng TamTheThangLong.
Cách tính đường cao trong tam giác đều
Tính đường cao trong tam giác đều dựa vào công thức Heron
Dưới đây là cách tính đường cao trong tam giác đều dựa vào công thức Heron. Mời bạn đọc cùng theo dõi để biết rõ hơn:
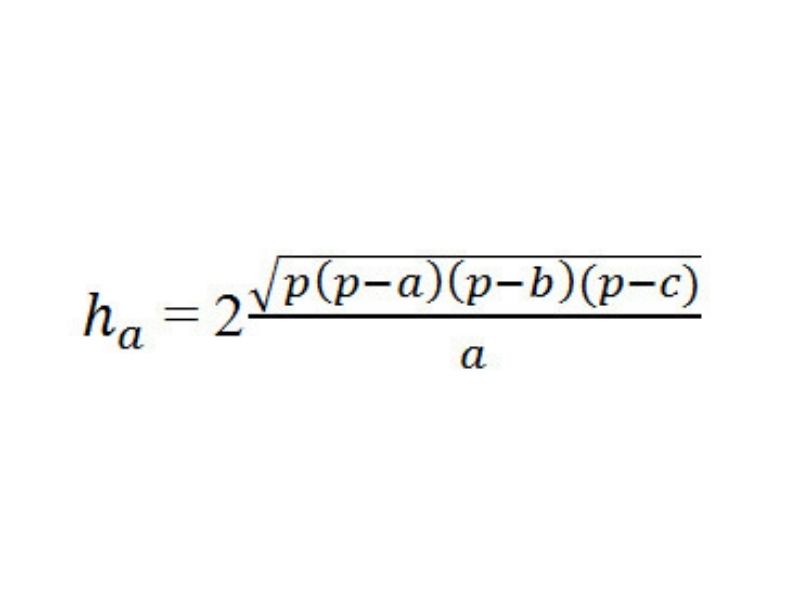
Trong đó:
- a, b, c: Lần lượt là độ dài các cạnh của tam giác.
- p: Nửa chu vi được tính theo công thức sau p = (a + b + c)/2.
- h: Chiều cao, ha là đường cao kẻ từ A xuống cạnh BC, hb là đường cao kẻ từ B xuống cạnh AC, hc là đường cao kẻ từ C xuống cạnh AB.
Thông tin trên của TamTheThangLong đã bật mí giúp bạn cách tính đường cao tam giác đều dựa vào công thức Heron. Bạn nên ghi nhớ công thức này để vận dụng vào bài tập một cách dễ dàng. Mời bạn đọc tiếp tục theo dõi phần nội dung cuối cùng của bài viết.
Tính đường cao trong tam giác đều dựa vào công thức tính đường cao trong tam giác cân
Sau đây là công thức tính đường cao tam giác đều dựa vào công thức tính đường cao trong tam giác cân. Mời bạn đọc theo dõi bài viết của TamTheThangLong để biết thêm chi tiết.
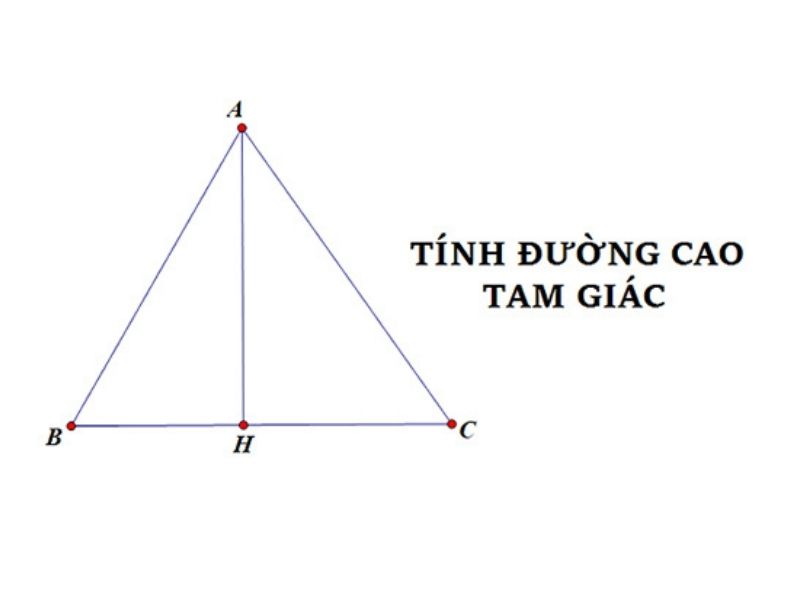
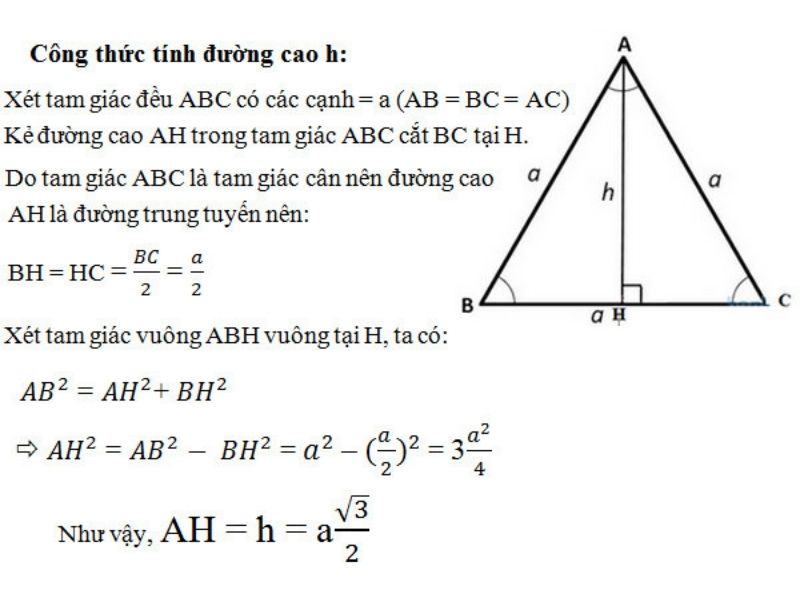
Xét tam giác đều ABC có các cạnh = a (AB = BC = AC). Kẻ đường cao AH trong trong tam giác ABC cắt BC tại H. Do tam giác ABC là tam giác cân nên đường cao AH là đường trung tuyến. Vì thế, chúng ta có công thức:
BH = HC = BC/2 = a/2.
Xét tam vuông ABH vuông tại H, ta có:
AB2 = AH2 + BH2
- AH2 = AB2 – BH2 = a2 – (a/2)2 = 3(a2/4)
- AH = h = a(/2)
Tam giác đều cũng là tam giác cân. Do đó, bạn có thể dựa vào đường cao của tam giác cân để tính đường cao của tam giác đều.
Xem thêm:
- Tính chất trọng tâm tam giác và cách xác định trọng tâm
- Tính chất ba đường cao của tam giác và bài tập áp dụng
Toàn bộ thông tin trên là những công thức về đường cao trong tam giác đều. Mong rằng bài viết của TamTheThangLong sẽ giúp cho các bạn dễ hiểu và ghi nhớ cách tính đường cao tam giác đều. Đừng quên truy cập TamTheThangLong thường xuyên để cập nhật những thông tin hay nhất nhé!
Trên đây là bài viết Công thức tính đường cao trong tam giác đều dễ nhớ nhất được Tâm Thế Thăng Long chia sẻ và cập nhật mới nhất. Chúc các bạn có những thông tin thật thú vị tại Tamthethanglong.com.