- 1. Đường tròn ngoại tiếp tam giác là gì?
- 2. Công thức tính bán kính đường tròn ngoại tiếp tam giác
- 3. Cách tính bán kính đường tròn ngoại tiếp tam giác
- 3.1 Sử dụng định lí sin trong tam giác
- 3.2 Sử dụng diện tích tam giác
- 3.3 Sử dụng trong hệ tọa độ
- 3.4 Sử dụng tam giác vuông
- 4. Bài tập về bán kính đường tròn ngoại tiếp tam giác
Bạn đang xem : Bán kính đường tròn ngoại tiếp tam giác là gì? Khái niệm
Bán kính đường tròn ngoại tiếp tam giác là gì? Khái niệm được cập nhật mới nhất tại Tamthethanglong.com. Trang thông tin tổng hợp mới nhất của giới trẻ hiện nay, cập nhật liên tục.
Trong Toán học, đường tròn ngoại tiếp tam giác có thể coi là một trong những phần vô cùng quan trọng. Vậy thì để hiểu chi tiết hơn về bán kính đường tròn ngoại tiếp tam giác, các bạn hãy cùng TamTheThangLong đi vào khám phá ngay dưới đây nhé!
Đường tròn ngoại tiếp tam giác là gì?
Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác. Từ đó, khi nối tâm O của đường tròn với ba đỉnh của tam giác ABC ta có được bán kính đường tròn ngoại tiếp của tam giác ABC là OA = OB = OC.
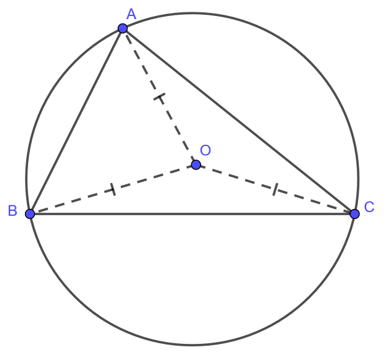
Tính chất của đường tròn ngoại tiếp tam giác:
Xem thêm : Dấu hiệu nhận biết hình thoi? Tính chất, các cách chứng minh
- Mỗi tam giác sẽ chỉ có duy nhất một đường tròn ngoại tiếp.
- Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
- Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
- Trong tam giác đều, tâm đường tròn ngoại tiếp và nội tiếp tam giác trùng nhau.
Công thức tính bán kính đường tròn ngoại tiếp tam giác
Các công thức tính bán kính đường tròn ngoại tiếp tam giác:
- Công thức tính bán kính đường tròn ngoại tiếp tam giác: R = (a x b x c) : 4S.
- Công thức tính bán kính đường tròn ngoại tiếp của góc A:
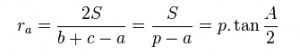
- Công thức tính bán kính đường tròn ngoại tiếp của góc B:
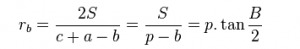
Tham khảo thêm : M là gì trong Hóa học? Một số công thức liên quan đến m và M
- Công thức tính bán kính đường tròn ngoại tiếp của góc C:
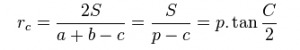
Trong đó:
- r: Bán kính đường tròn ngoại tiếp tam giác
- S: Diện tích tam giác.
- a, b, c: Độ dài các cạnh của hình tam giác.
- A, B, C: Các góc của hình tam giác.
Cách tính bán kính đường tròn ngoại tiếp tam giác
Có rất nhiều cách khác nhau để tính bán kính đường tròn ngoại tiếp tam giác. Sau đây là một số cách phổ biến.
Sử dụng định lí sin trong tam giác
Cách đầu tiên chính là sử dụng định lí sin trong tam giác để tính bán kính đường tròn ngoại tiếp tam giác.
Ví dụ: Cho tam giác ABC có BC = a, CA = b và AB = c, R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó:
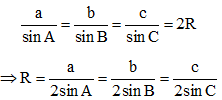
Trong đó có:
- R: Bán kính đường tròn ngoại tiếp tam giác
- a, b, c: Độ dài các cạnh của hình tam giác.
- A, B, C: Các góc của hình tam giác.
Sử dụng diện tích tam giác
Bên cạnh cách dùng định lý sin, chúng ta cũng có thể sử dụng diện tích trong tam giác để tính bán kính đường tròn ngoại tiếp tam giác:
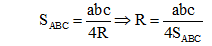
Trong đó có:
- R: Bán kính đường tròn ngoại tiếp tam giác.
- S: Diện tích tam giác.
- a, b, c: Độ dài các cạnh của hình tam giác.
- A, B, C: Các góc của hình tam giác.
Sử dụng trong hệ tọa độ
Ngoài ra, tính bán kính đường tròn khi sử dụng trong hệ tọa độ cũng là một cách được rất nhiều người ưa chuộng. Sau đây là các bước cơ bản để tính bán kính:
- Tìm tọa độ tâm O của đường tròn ngoại tiếp tam giác ABC.
- Tìm tọa độ một trong ba đỉnh A, B, C (nếu chưa có).
- Tính khoảng cách từ tâm O tới một trong ba đỉnh A, B, C, đây chính là bán kính cần tìm: R=OA=OB=OC.
Sử dụng tam giác vuông
Sử dụng tam giác vuông để tính bán kính có lẽ là cách cơ bản nhất. Tâm của đường tròn ngoại tiếp trong tam giác vuông là trung điểm của cạnh huyền.
Do vậy, bán kính đường tròn ngoại tiếp tam giác vuông là bằng nửa độ dài của cạnh huyền đó.
Bài tập về bán kính đường tròn ngoại tiếp tam giác
Nhằm hiểu sâu hơn về bài học, chúng ta sẽ cùng nhau đi đến các bài tập về bán kính đường tròn ngoại tiếp tam giác.
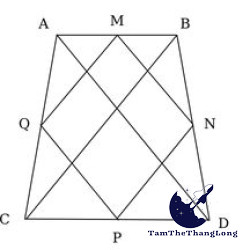
Bài tập 1: Cho tam giác MNP vuông tại N, và MN = 6cm, NP = 8cm. Xác định bán kính đường tròn ngoại tiếp tam giác MNP bằng bao nhiêu?
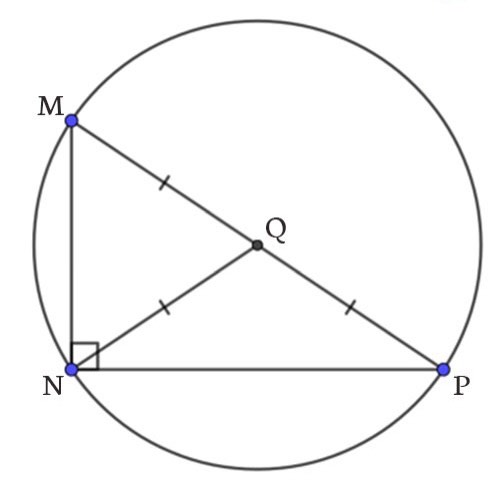
Áp dụng định lý Pytago, ta có:
PQ = 1/2 MP
=> NQ = QM = QP = 5cm
Gọi D là trung điểm MP.
=> ∆MNP vuông tại N có NQ là đường trung tuyến ứng với cạnh huyền MP
=> Q là tâm đường tròn ngoại tiếp ∆MNP
=> Đường tròn ngoại tiếp ∆MNP là trung điểm Q của cạnh huyền và bán kính đường tròn ngoại tiếp MNP là R = MQ = 5cm
Bài tập 2: Cho tam giác ABC có góc B bằng 45° và AC = 4. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC.
Ta có: b = AC = 4
Áp dụng định lý sin trong tam giác ABC ta có:
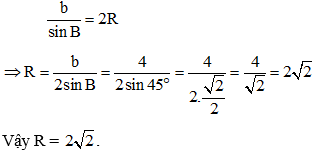
Bài tập 3: Cho tam giác MNP có MN = 6, MP = 8 và PN = 10. Tính bán kính đường tròn ngoại tiếp tam giác MNP.
Ta có: MN² + MP² = 6² + 8² = 36 + 64 = 100.
mà PN² = 10² = 100.
=> MN² + MP² = PN².
Do đó tam giác MNP vuông tại M (định lý Pytago đảo).
Vậy bán kính đường tròn ngoại tiếp tam giác MNP là :
R = 1/2 PN = 1/2.10 = 5.
Bài tập 4: Cho tam giác MNP đều với cạnh bằng 12cm. Xác định tâm và bán kính đường tròn ngoại tiếp ∆MNP?
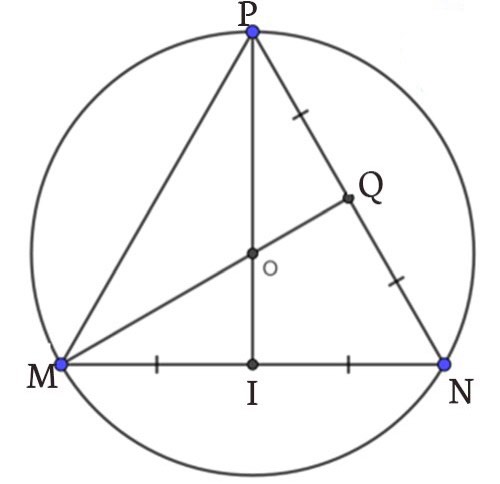
Gọi Q, I lần lượt là trung điểm của cạnh NP, MN và MQ giao với PI tại O.
Vì ∆MNP đều nên đường trung tuyến cũng là đường cao, đường phân giác, đường trung trực của tam giác.
=> O là tâm của đường tròn ngoại tiếp.
=> ∆MNP có PI là đường trung tuyến nên PI cũng là đường cao.
Từ đó áp dụng định lý Pytago:
PI² = MP² – MI² = 122 – 62 = 108 (cm).
=> PI = 6√3cm.
Bởi O là trọng tâm của ∆MNP nên:
PO = 2/3 PI = 2/3 x 6√3 = 4√3 (cm).
Như vậy qua bài viết trên, chắc hẳn các bạn cũng đã biết cách tính bán kính đường tròn ngoại tiếp tam giác rồi phải không nào? Vậy thì các bạn hãy mau chóng theo dõi TamTheThangLong ngay để cập nhật thêm nhiều thông tin thú vị hơn nữa nhé!
Trên đây là bài viết Bán kính đường tròn ngoại tiếp tam giác là gì? Khái niệm được Tâm Thế Thăng Long chia sẻ và cập nhật mới nhất. Chúc các bạn có những thông tin thật thú vị tại Tamthethanglong.com.